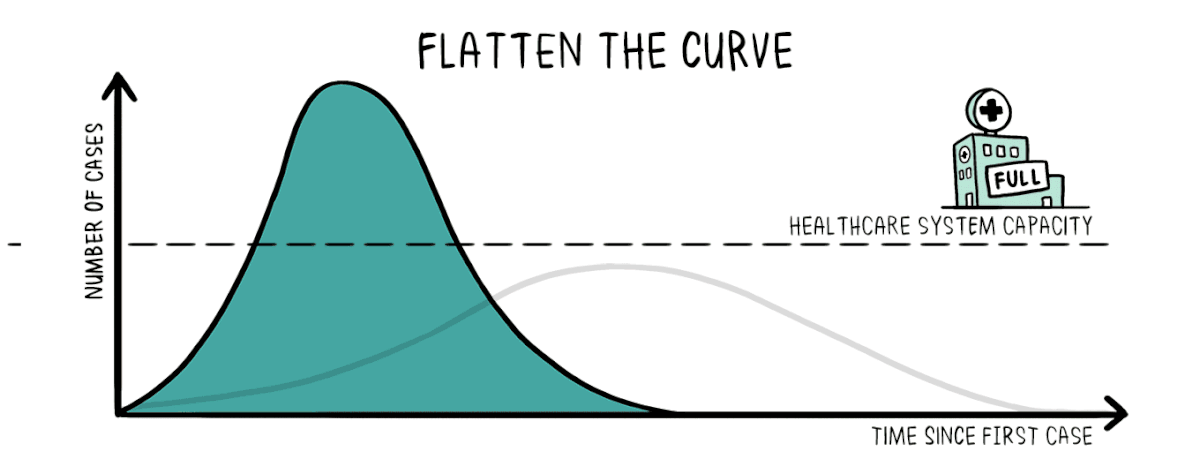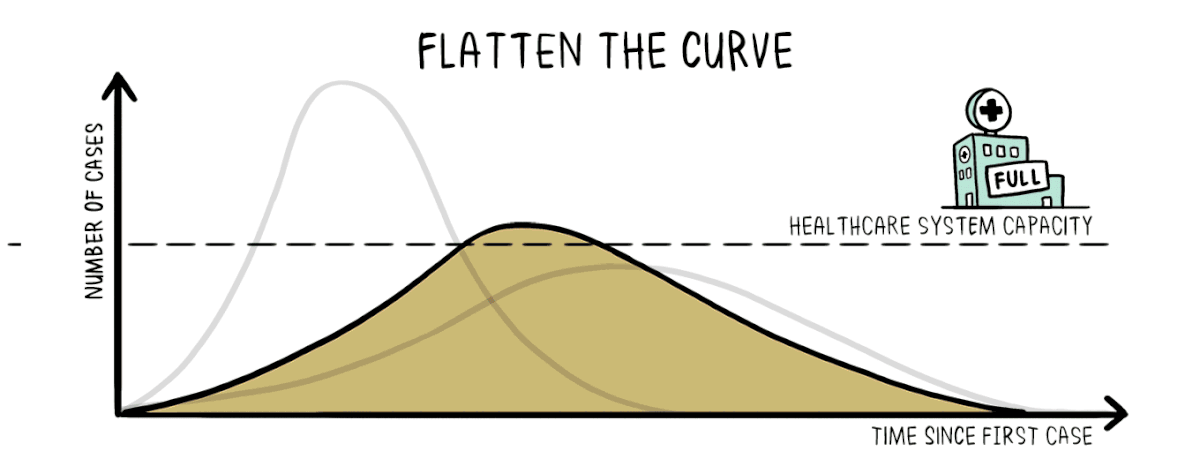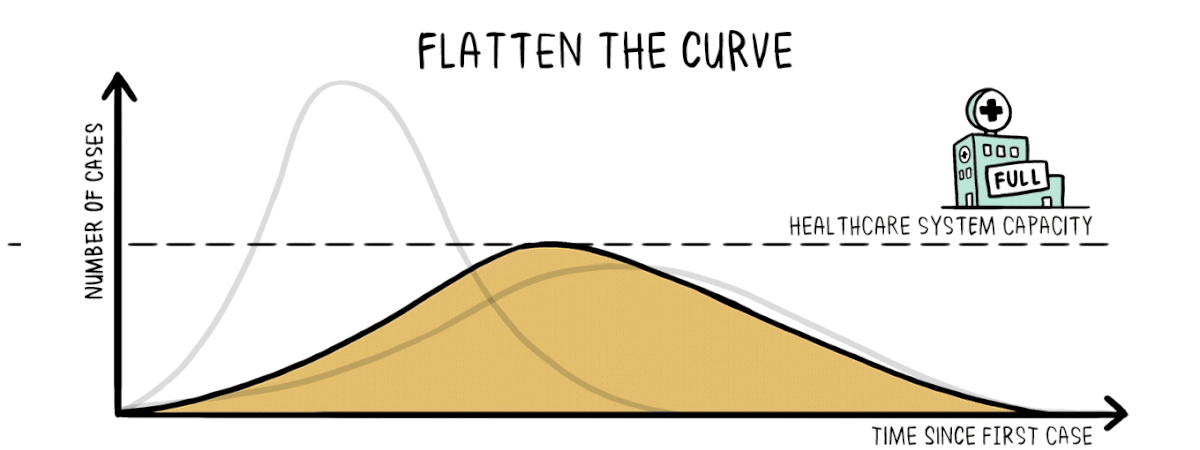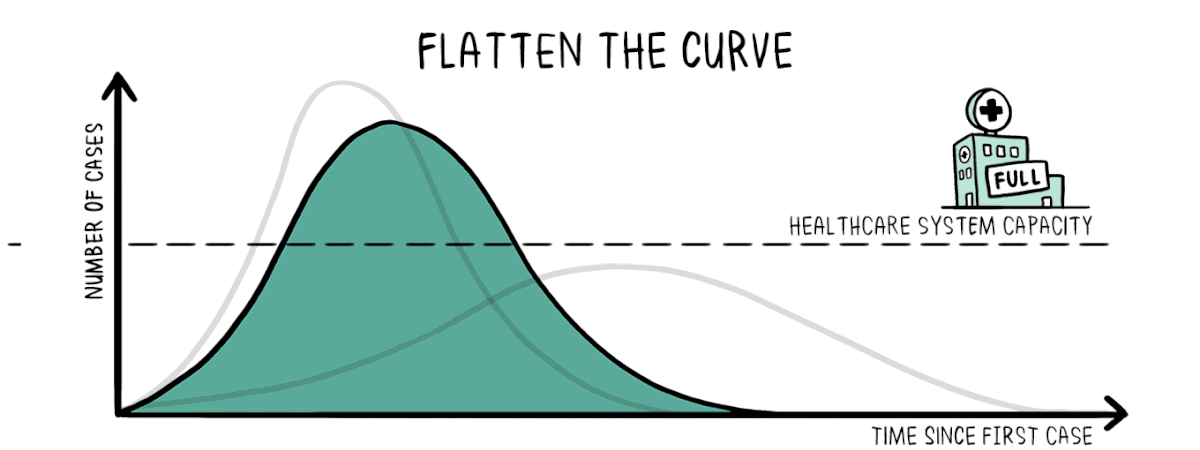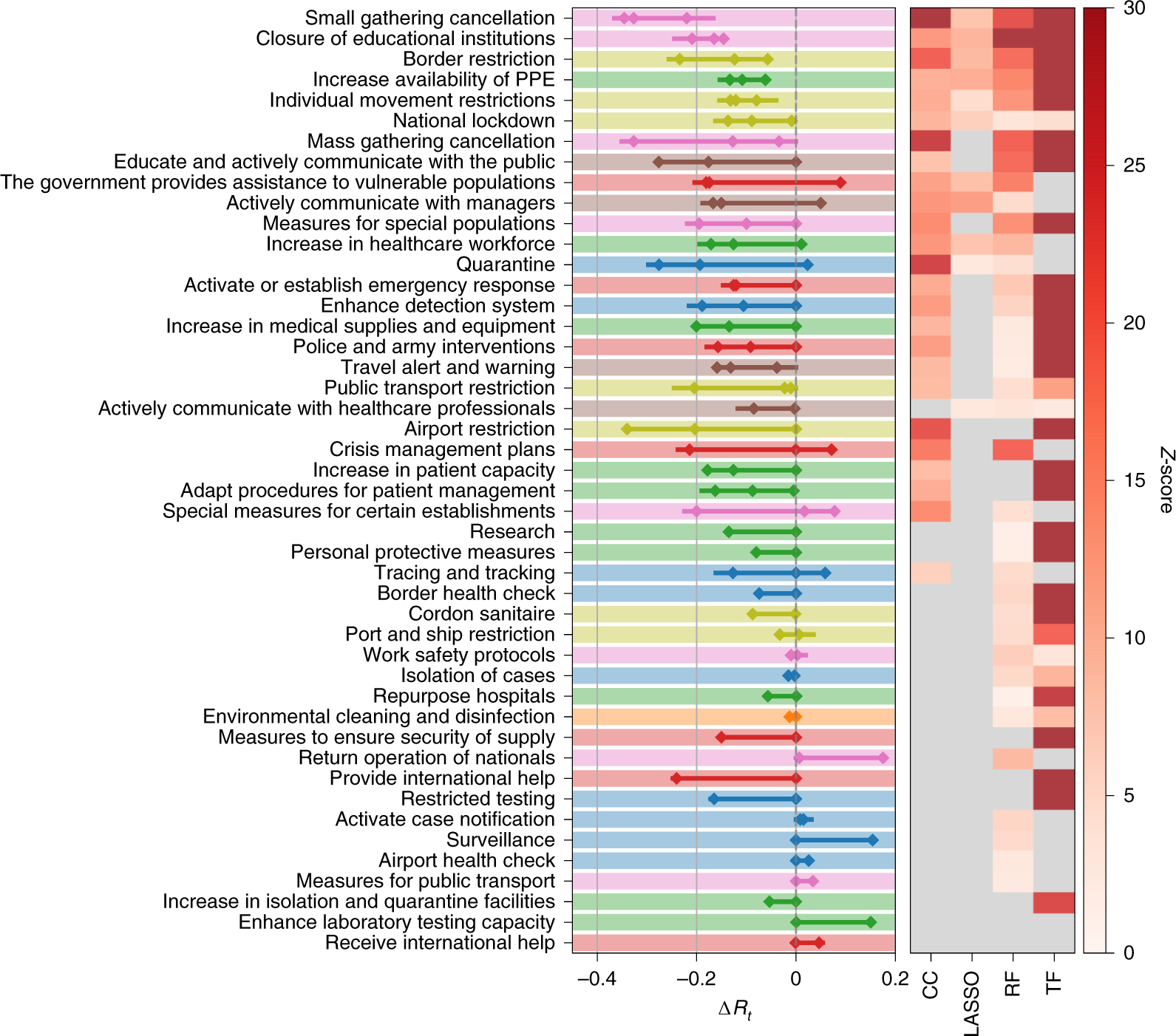

Fonte: Nature. Classifica dell’efficacia degli interventi contro il COVID-19 a livello mondiale.
La valutazione dell’efficacia degli interventi non farmaceutici (NPI) per mitigare la diffusione del SARS-CoV-2 è fondamentale per informare i futuri piani di risposta.
Il Grafico mostra gli intervalli di confidenza al 95% combinati di ΔRt per gli interventi più efficaci in tutti i territori. La mappa di calore nella parte destra del pannello mostra i punteggi Z corrispondenti all’efficacia della misura determinati dai quattro diversi metodi.
Gli NPI (Interventi Non Farmaceutici) sono classificati in base al numero di metodi che concordano sul loro impatto, dall’alto (più significativo in tutti i metodi) al basso (inefficace in tutte le analisi).
I temi L1 sono codificati a colori. Il grigio non indica alcun effetto positivo significativo.
Lo studio pubblicato su Nature quantifica l’impatto di 6.068 NPI codificati gerarchicamente ed implementati in 79 territori, con il numero di riproduzione effettiva Rt, di COVID-19.
L’ approccio di modellazione combina quattro tecniche computazionali che uniscono strumenti statistici, inferenziali e di intelligenza artificiale.
I risultati sono convalidati attraverso due set di dati esterni che registrano 42.151 NPI aggiuntivi da 226 paesi. I risultati indicano che è necessaria un’adeguata combinazione di NPI per frenare la diffusione del virus. Gli NPI meno distruttivi e costosi possono essere efficaci quanto quelli più intrusivi e drastici (ad esempio, un blocco nazionale).
Utilizzando scenari “what-if” specifici per Paese, si valuta come l’efficacia degli NPI dipenda dal contesto locale, come i tempi della loro adozione, aprendo la strada alla previsione dell’efficacia degli interventi futuri.
Emerge un quadro chiaro dove i temi dell’allontanamento sociale e delle restrizioni di viaggio sono i primi classificati in tutti i metodi, mentre le misure ambientali (ad esempio, la pulizia e la disinfezione delle superfici condivise) sono classificate come meno efficaci.
TECNICHE DI REGRESSIONE
Per quantificare l’impatto di un intervento NPI, sono stati usati quattro diversi approcci statistici applicati sulla riduzione di Rt (Informazioni supplementari).
Analisi CC (Caso Controllo)
L’analisi caso-controllo considera ogni singola categoria (L2) o sottocategoria (L3) separatamente e valuta la differenza, ΔRt, in Rt tra tutti i Paesi che hanno implementato M (casi) e quelli che non l’hanno fatto (controlli) durante il finestra di osservazione.
L’abbinamento viene effettuato in base all’età dell’epidemia e al tempo di attuazione dell’eventuale risposta. Viene contemplato anche il ritardo di τ giorni tra l’implementazione di M e l’osservazione di ΔRt come ulteriori covariate nazionali che quantificano altre dimensioni di governance e sviluppo umano ed economico.
Le stime per Rt sono calcolate in media su ritardi compresi tra 1 e 28 giorni.
Funzione Step Regressione Lazo
In questo approccio assumiamo che, senza alcun intervento, il fattore di riproduzione sia costante e le deviazioni da questa costante derivano da un inizio ritardato di τ giorni di ogni NPI su L2 (categorie) del dataset gerarchico.
Si usa un approccio di regolarizzazione lazo combinato con una ricerca di meta parametri per selezionare un insieme ridotto di NPI che meglio descrivono il ΔRt osservato.
Le stime per le variazioni di ΔRt attribuibili a NPI M sono ottenute da una convalida incrociata a livello di paese.
Regressione RF
Si esegue una regressione RF, in cui gli NPI implementati in un paese vengono utilizzati come predittori per Rt, giorni τ spostati nel tempo nel futuro.
Qui, τ rappresenta il ritardo tra l’implementazione e l’inizio dell’effetto di un dato NPI. Analogamente alla regressione Lazo, l’assunto alla base dell’approccio RF è che, senza modifiche negli interventi, il valore di Rt in un territorio rimane costante.
Tuttavia, contrariamente ai due metodi descritti sopra, RF rappresenta un modello non lineare, il che significa che gli effetti dei singoli NPI su Rt non devono sommarsi linearmente.
L’importanza di un NPI è definita come il calo delle prestazioni predittive della RF su dati invisibili se i dati relativi a tale NPI vengono sostituiti dal rumore, chiamato anche importanza di permutazione.
Modellazione di trasformatori
I Transformatori sono stati dimostrati come modelli adatti a processi dinamici a elementi discreti come sequenze testuali, grazie alla loro capacità di ricordare eventi passati. Qui abbiamo esteso l’architettura del trasformatore per avvicinarsi al caso continuo di dati epidemici rimuovendo lo strato di uscita probabilistico con una combinazione lineare di uscita del trasformatore, il cui ingresso è identico a quello per la regressione RF, insieme ai valori di Rt.
La rete con le migliori prestazioni (errore quadratico medio minimo nella convalida incrociata per paese) è identificata come un trasformatore codificatore con quattro strati nascosti di 128 neuroni, una dimensione di incorporamento di 128, otto teste, un output descritto da uno strato di output lineare e 47 ingressi (corrispondenti a ciascuna categoria e Rt).
Per quantificare l’impatto della misura M su Rt, è stato utilizzato il trasformatore addestrato come modello predittivo, e confrontate le simulazioni senza alcuna misura (riferimento) con quelle in cui viene presentata una misura alla volta per valutare ΔRt.
Per ridurre gli effetti dell’overfitting e della molteplicità dei minimi locali, riportiamo i risultati di un insieme di trasformatori addestrati a livelli di precisione simili.
Stima di Rt
Si è usato il pacchetto R EpiEstim con una finestra temporale scorrevole di 7 giorni per stimare le serie temporali di Rt per ogni paese.
Si è scelto un intervallo seriale incerto seguendo una distribuzione di probabilità con una media di 4,46 giorni e una deviazione standard di 2,63 giorni.
Classifica degli NPI
Per ciascuno dei metodi (CC, regressione Lazo e TF), classifichiamo le categorie NPI in ordine decrescente in base al loro impatto, ovvero al grado stimato in cui riducono Rt o all’importanza delle loro caratteristiche (RF).
Per confrontare le classifiche, contiamo quanti dei 46 NPI considerati sono classificati come appartenenti alle prime x misure classificate in tutti i metodi si testa l’ipotesi nulla che questa sovrapposizione sia stata ottenuta da classifiche completamente indipendenti.
Il valore P è quindi dato dalla funzione di distribuzione cumulativa complementare per un esperimento binomiale con 46 prove e probabilità di successo (x / 46) 4. Si riporta il valore P mediano ottenuto su tutti x ≤ 10 per garantire che i risultati non dipendano da dove imponiamo il cut-off per le classi.
Rete di co-implementazione
Se esiste una tendenza statistica secondo cui un paese che implementa l’NPI i implementa anche l’NPI j in un secondo momento, tracciamo un collegamento diretto da i a j.
I nodi sono posti sull’asse y in base all’età media dell’epidemia alla quale viene implementato il corrispondente NPI; sono raggruppati sull’asse x dal loro tema L1. I colori dei nodi corrispondono ai temi. L’efficacia dei punteggi per tutti gli NPI vengono ridimensionati tra 0 e 1 per ciascun metodo; la dimensione del nodo è proporzionale ai punteggi ridimensionati, mediati su tutti i metodi.